Below are the techniques used on how to calculate correction factors in a calibration result that you can use.

1. Direct application using the Correction value

2. Using the Nearest Reported Correction Value in the Certificate

3. Averaging Between 2 Correction Factors

4. Using Linear Interpolation to Determine Any Value Between 2 Points

There are other methods and correction factor formulas out there but these 4 are the simplest and the only method I use as per my experience.

1. Direct Application using the “Correction” Value

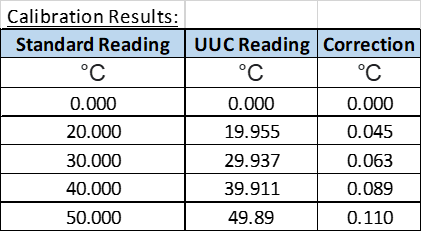
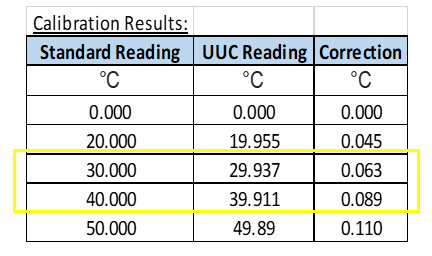
sample calibration result showing the values of calculated “correction”

The Correction Factor formula for calibration is:

Correction = (True Value) – (Measured Value)

Correction = Correction Factor (CF)

     CF = – Error

Example above @20 °C range:

Correction = 20.000 – 19.955 = 0.045 °C

CF = 0.045 °C

2. Using the Nearest Reported Correction Value in the Certificate

This is the technique that I can say is based on common sense to determine the correction factor.

You can apply this technique if a small difference does not have a significant impact on the results, or it is negligible because of a wide tolerance limit or the effect of resolution (low-resolution instrument), then this is a quick way to determine and estimate the correction factor.

If the measured value you need is not in the middle but very close to either the upper or lower range, just choose the one where it is closer.

See the below example.

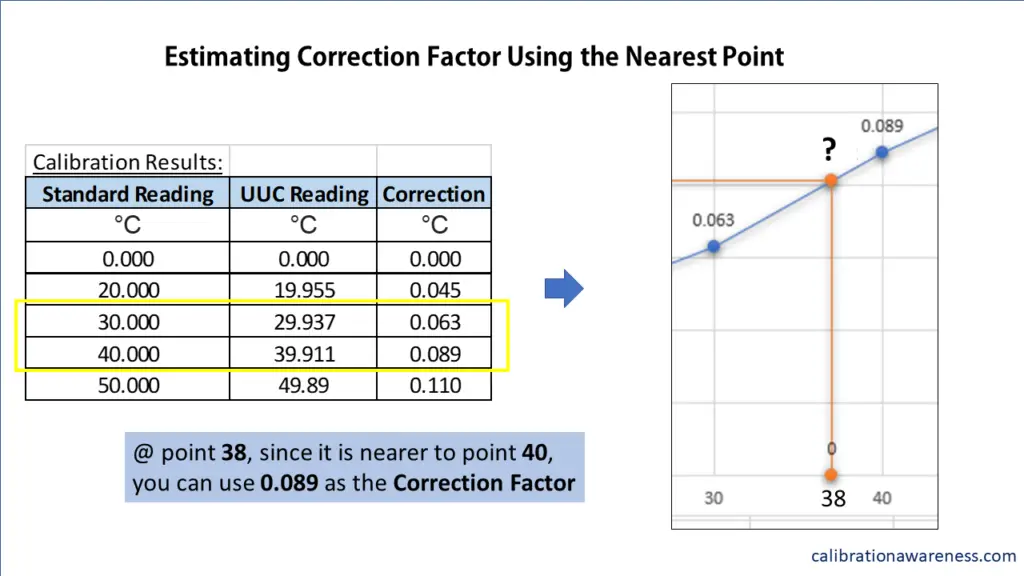
How to Determine the correction factor if the exact value you need is not given? Or, how to adjust the correction factor to have the exact value you need?

To answer these, let us discuss the next 2 techniques, read more below…

3. Averaging Between 2 Correction Factors

If you only need to calculate the value of a correction factor between 2 successive points, you can use the Averaging Method. Just add the 2 successive points then divide it by 2. See the below example using the same data points above:

For example, we need the CF of the value equal to 25

The values that we need are the Correction Factor between 20 and 30 which are equal to 

0.045 and 0.063. 

Now we can calculate the CF for Standard Reading at 25

CF = [(0.045)+(0.063)]/2

CF= 0.0108/2

CF = 0.054

4. Using Linear Interpolation to Determine Any Value Between 2 Points

If 2 points are given (which are the Max and Min points) with Correction value in an increasing (or decreasing) manner, we can calculate any value in between using Linear Interpolation.

Linear Interpolation is best used when we want to determine the value that lies anywhere in a given range bounded by Max and Min points.

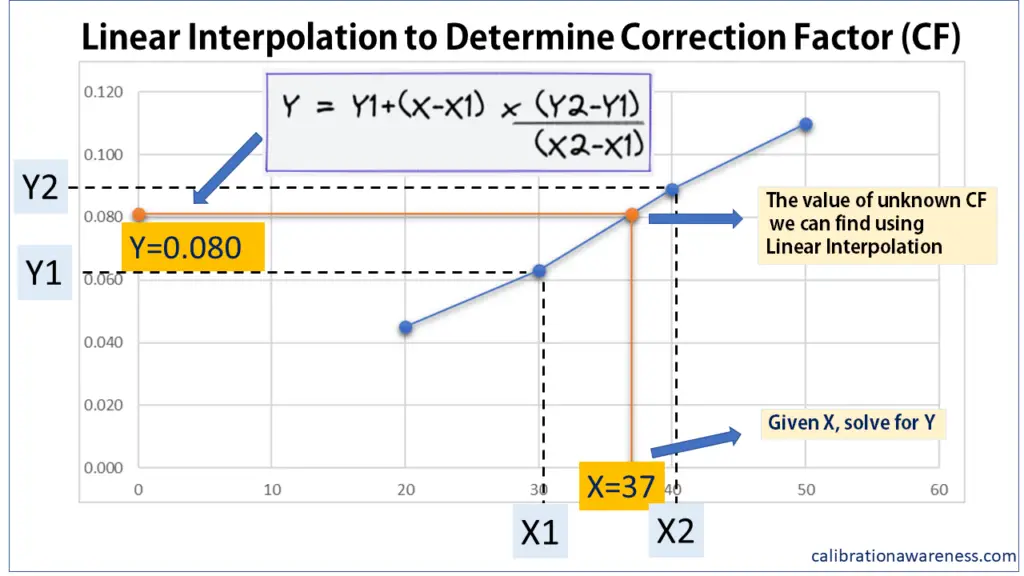
Graphical representation and formula for Linear Interpolation were used to determine the Correction Factor at the standard reading of 37 given the upper and lower values.

The equation for a linear Interpolation is:

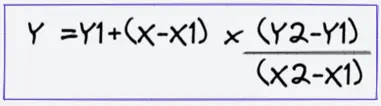
Where:

X1 and X2 are the given Standard Readings

Y1 and Y2 are the equivalent Correction Factors (or correction value)

X =The required standard value where Correction Factor is needed

Y = the calculated Correction Factor based on X

For example, determine the Correction factor @ point 37 in the table below (You can refer to the graph above):

Conclusion

One of the most important skills when interpreting and using a calibration result is the capability to understand and calculate Correction Factors. One good reason is for us to appreciate more the importance of a calibration result by achieving the most accurate measurements.

Correction Factor helps us achieve more accurate measurement results by simply compensating for the error.

Correction factor is also known as calibration correction and/or corrective factors. The value of correction factors comes from the calculated “correction” which is the opposite of “error”.